buyssetr.blogg.se - Appropriate names for a line geometry

#Appropriate names for a line geometry how to

If two distinct planes are perpendicular against a common line, then these two planes must be parallel to each other.Įxample 1: A teacher has drawn a plane on the whiteboard and has asked Mason to name the plane while also mentioning the coplanar and collinear points.

If two lines are perpendicular against the same plane, then these two lines will be parallel to each other.

If there are two planes, they can either be parallel or perpendicular to each other.

The line can either be perpendicular, parallel or lie in the plane.

Hence, the points of a plane are non-collinear.

A plane consists of three coplanar points which do not lie on the same line.

The properties of a plane are given below. For example, Planes S and A intersect, and the common line between them is line XY, as shown in the picture below. This means that only a single line will be common between the two planes. The planes cannot intersect with each other for more than one line. These planes are perpendicular to each other, meaning one plane passes through the second plane at $90^$. Intersecting Planes: These are the planes which intersect with each other. Similarly, walls on both sides of the room can also be considered parallel planes. For example, the floor and ceiling of a room with indefinite boundaries can be considered parallel planes. Parallel Planes: The planes that do not intersect are known as parallel planes. There are two types of planes in geometry: a) Parallel Plane and b) Planes that intersect.

A single plane can pass through only three non-collinear but coplanar points. It does not wobble much, but the moment we add the fourth leg, it starts to wobble the same is true with the plane.

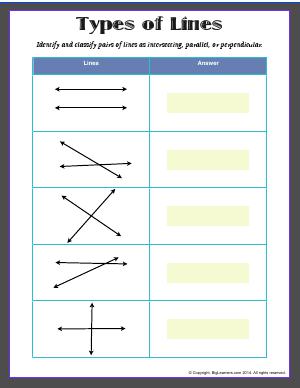
We know it has three legs, and even if they are not equal in length, the tripod works just fine. Just for fun’s sake, let’s take an example of a tripod. Hence, we only take three non-collinear but coplanar points for a plane. But suppose it is coplanar and the plane passes through it along with the first two points, then the plane will not pass through the previous third point. When we add the fourth point, then it can either be coplanar or non-coplanar if it is not coplanar, then it is not even on the plane. So what happens when we add the fourth point in the plane is that either the point will be coplanar with other given points or it will not lie in the plane, simple as that. But if the three points are non-collinear, then one and only one plane can pass through it. Now to the second question, why can’t a plane consist of four non-collinear points? If we take two points, then it gives a 1-dimensional line which we can rotate in a plane, and if we add a third point which is collinear to the previous two points, then infinite planes can pass through these points. Let us answer these questions one by one why can a plane not have two non-collinear points? Because the 2 points are always collinear and you can draw a straight line by connecting two points no matter where they are present in a plane, as shown in the picture below.

#Appropriate names for a line geometry how to

Can a flat surface with 2 or 4 points be called a plane, or how to name a plane with 4 points? So how many points are required to name a plane? As already discussed, a flat surface having three non-collinear points is a plane. Identifying a plane is easy as we need to identify a flat surface with multiple points in it. As discussed earlier, a plane consists of three non-collinear points, so if we plot three points in the parallelogram so that those points do not lie on the same line, then we will say that this parallelogram represents a plane. Remember that we can also draw a plane on a three-dimensional surface, but we will keep our discussion related to the two-dimensional systems in this topic. Suppose we have drawn the parallelogram on a two-dimensional surface. As there are no real-life examples, we will take a flat piece of paper and draw a parallelogram on it along with many lines, which shows the infinite nature of the surface because lines are infinite and have no depth or curvature, just like a plane. Let us now model a concept of a plane in the shape of a geometrical figure. For example, the flat surfaces of a square, cube or piece of paper are considered real-life examples of a plane if the boundaries are considered infinite. Read more Halfplane: Definition, Detailed Examples, and MeaningĪ commonly asked question can we see a plane in real life? Well, it is impossible to see a plane as we already said, it does not have any boundaries, but we can imagine some surfaces to be considered a plane if they are not limited by boundaries.